Time to Read 6 min
Do you have to design an industrial data acquisition system and don't know how to configure the filters? Are you struggling with noise and interference in your product and don't know how to reduce it? Have you ever wondered if analog or digital filters are better?
These questions occur in practice again and again. An analog sensor should be connected to a digital control loop or to a data acquisition system. If there are problems with the measured signal, the call for an analog filter to eliminate the problem follows quickly. But is this also the right way? After all, it is very complex to adapt an analog filter to new requirements (except SC (Switched Capacitor) filters). Also the necessary space for an analog filter should not be underestimated. The following description shows you how you can judge for yourself whether you need additional measurement filters and whether they are correctly dimensioned.
Typical Situations
The questions mentioned above can occur in very different situations, e.g:
- Production and testing: Here, data acquisition systems from National Instruments and other manufacturers are often used. This reduces the development effort tremendously. However, these systems often do not have adaptable, analog filters. Long test leads can also capture additional interference.
- Product development: There is hardly a product that does not have sensors and subsequent digitization. The data acquisition system is often reduced to an integrated analog-digital converter. Component costs, space requirements as well as the power consumption of the product are often important. Analog filters cause additional costs and require space. Digital filters on the other hand can increase power consumption.
Sources of Interference
Interference of the measured signal can occur both in the sensor and on the transmission line to the data acquisition system. Depending on the physical process and the measuring principle used, significant noise can also be generated in the sensor itself. For the sake of simplicity, we assume here that noise tends to be rather broadband, but interference tends to be narrowband.
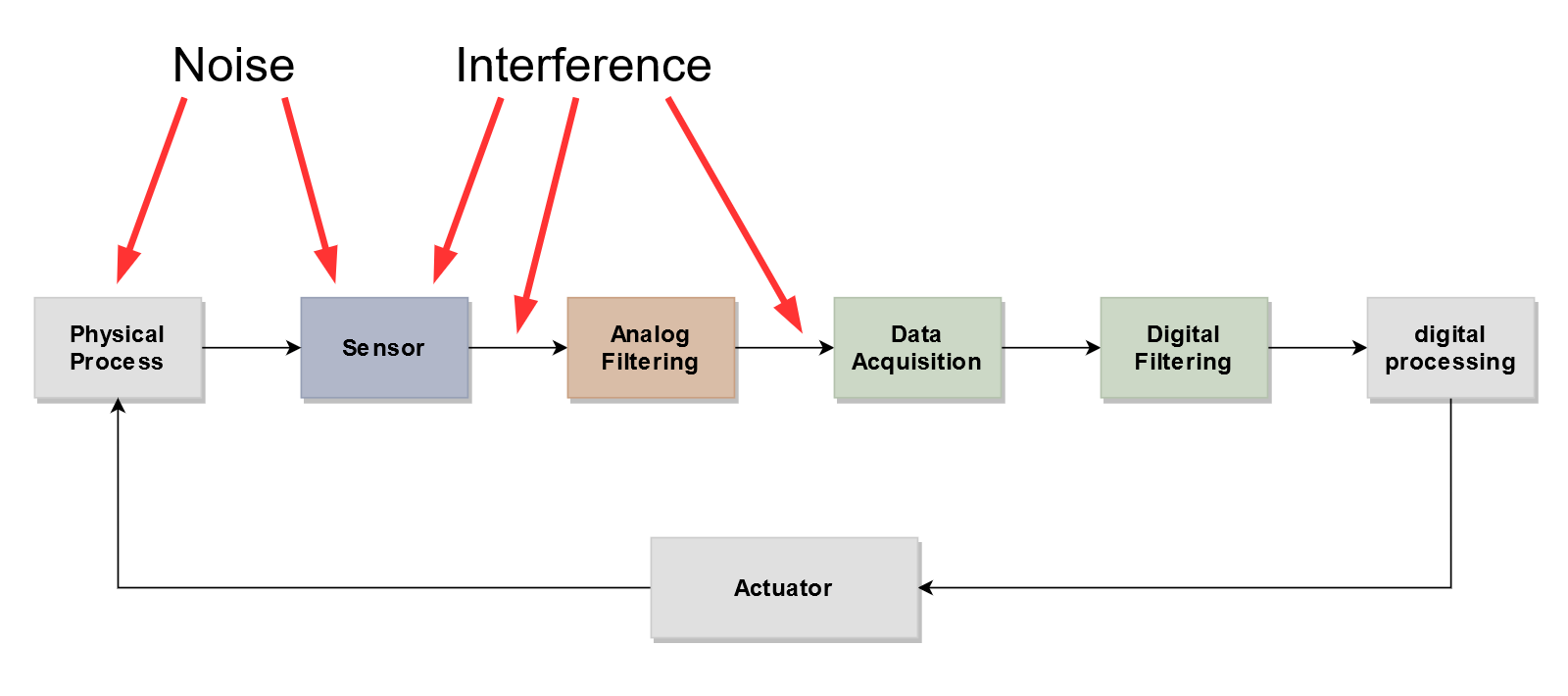
Reasons for an Analog Filter
Analog filters are inserted between sensor and A/D converter for two different reasons:
- Case A: To reduce interference and noise outside the useful band of the sensor signal
- Case B: To prevent aliasing during digitization
In Case A the analog filter can be replaced by a digital filter in most cases. It is always possible to design a digital filter so that it has largely the same properties as an analog filter. So both types of filters are interchangeable. (The only exception: the interference is so strong that it leads to clipping or other non-linear effects before digitization).
Thanks to the high computing power of today's data acquisition systems, there is no reason to implement such filters in the analog domain anymore. A correctly performed digital reduction of the sampling rate with carefully selected digital low pass filters can reduce the noise at least equally well.
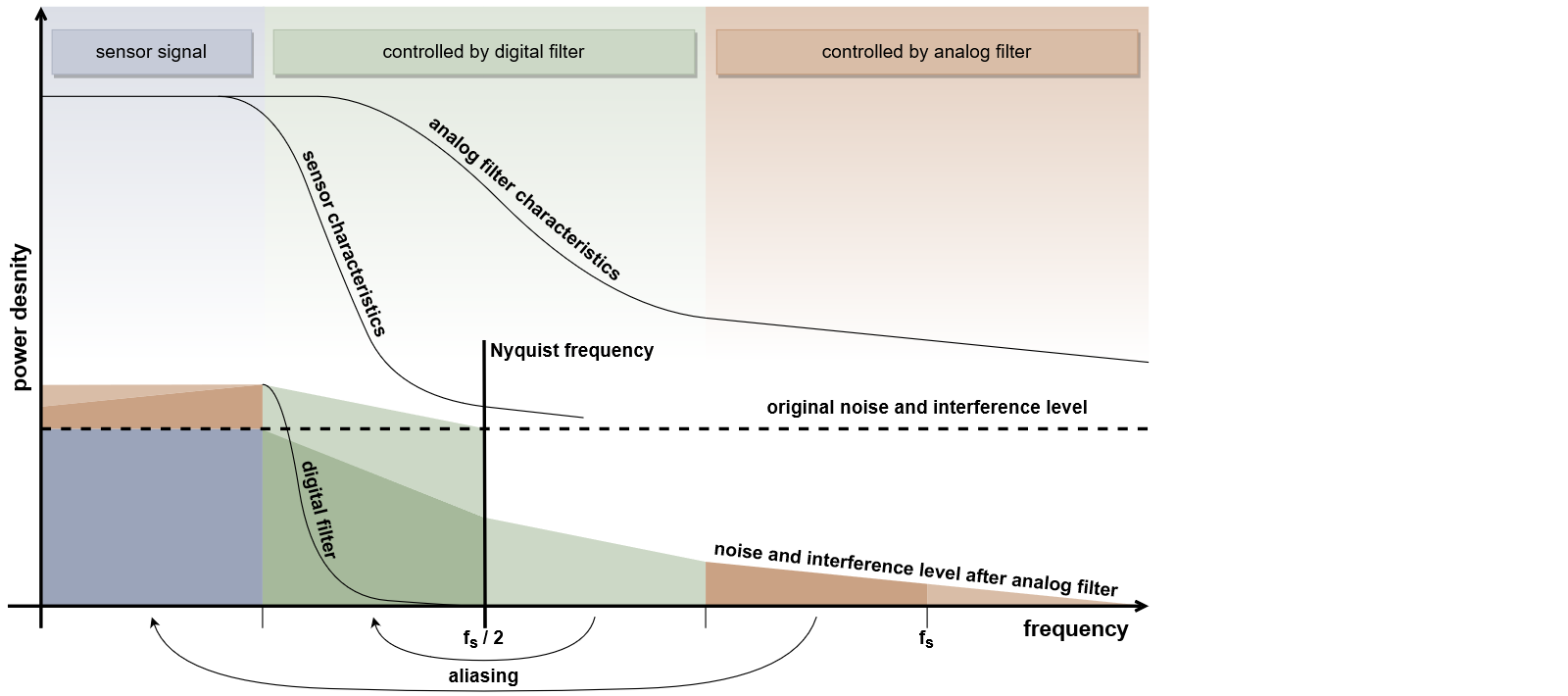
In Case B you have to consider whether aliasing effects occur in your application to a significant extent at all. The small signal bandwidth of most sensors together with a comparatively high sampling rate ensures that the sensor itself already acts as an anti-aliasing filter for high-frequency signal components. The additional analog anti-aliasing filter only has to attenuate noise and disturbances that are far above the Nyquist frequency to such an extent that they are not mirrored into the signals band.
The optimum is reached when the attenuation is so high that small signals are no longer obscured by the aliasing. The frequency range near the sampling rate is crucial. Only if your sensor signal has significant noise components here, you need an analog filter. And only for this frequency range you have to design the analog filter. You can also shift already known narrowband sources of interference by clever choice of the sampling rate into frequency ranges where they can be filtered away more easily.
The higher you choose the sampling rate of the system, the easier the design of the analog anti-aliasing filter becomes. Even if your sensor should produce high-frequency signal components, it is usually easier to increase the sampling rate instead of designing a complex analog filter. Once the sensor signal is digitized, you can reduce the sampling rate to the desired value. See Case A.
Fast Data Acquisition Systems
Fortunately, industrial sensors for physical quantities usually have a very narrow signal bandwidth compared to the connected data acquisition system. Due to this fact, analog filters are no longer necessary in many cases. If the sampling rate is high enough, a subsequent digital filtering or a reduction of the sampling rate is usually sufficient.
Further Criteria
Digital filters can be adapted very quickly to new requirements. However, if the filter order increases in the process, this also affects the required computing power and, in embedded systems, the power consumption. Compared to analog filters, digital filters also have the advantage that filter topologies which cannot be implemented as analog filters are possible, e.g. filters with very high steepness or FIR filters. The latter have advantages especially if you want to better control not only the frequency response but also the phase response or group delay.
Filters in Control Loops
High group delays make the design of control loops more complex and lead to an unstable controller in the worst case. Again, the principle applies that equivalent digital filters and analog filters have the same group delay. Nevertheless, digital filters more often lead to instability in fast control loops. However, this is not caused by the filter, but by the PC-based data acquisition systems which usually process the individual samples in blocks. This leads to large latency or dead times in the control loop. In such a case the block size must be adapted to the application.
Analog Filter Design is getting Easier and Easier
From the above it can be concluded that you can solve almost all measurement problems with an analog 1st order filter. Often you can even do without an analog filter completely and connect the sensor directly to the data acquisition system. In order to make the evaluation of data acquisition systems even easier, we have created a flow chart for you. It contains the most important questions of this blog in compact form: Antialiasing Selection Flow Chart.
And one last tip: Only use digital moving-average filters if you know the frequency of the interfering signal exactly and can adjust the filter length accordingly. In all other cases there are more effective solutions.
Ask one of our experts if you have problems with the analog or digital processing of sensor signals.
Daniel Megnet
Do you have additional questions? Do you have a different opinion? If so, email me or comment your thoughts below!
No Comments