Wie mit Unschärfe umgehen?

Wahrscheinlichkeitsverteilung (lognormal)

Jetzt möchte man natürlich nicht bei jedem Arbeitspaket über die exakte Kurve diskutieren, daher nimmt man gewisse Kurvenformen als Modell an, die sich mit wenigen Parametern beschreiben lassen.

In den nächsten Abschnitten werden verschiedene Ansätze dazu diskutiert:

• Dreipunktschätzung: Der genaue Weg
• Zweipunktschätzung: Wie es einfacher geht, mit Optimismuskompensation
• Lognormalverteilung: Eine asymetrische Verteilung
• Das 90%-Konfidenzintervall: Wie viel Risiko hätten Sie denn gern?
• Zentraler Grenzwertsatz: Wie viele ungenaue Schätzungen zum genaue Resultat führen

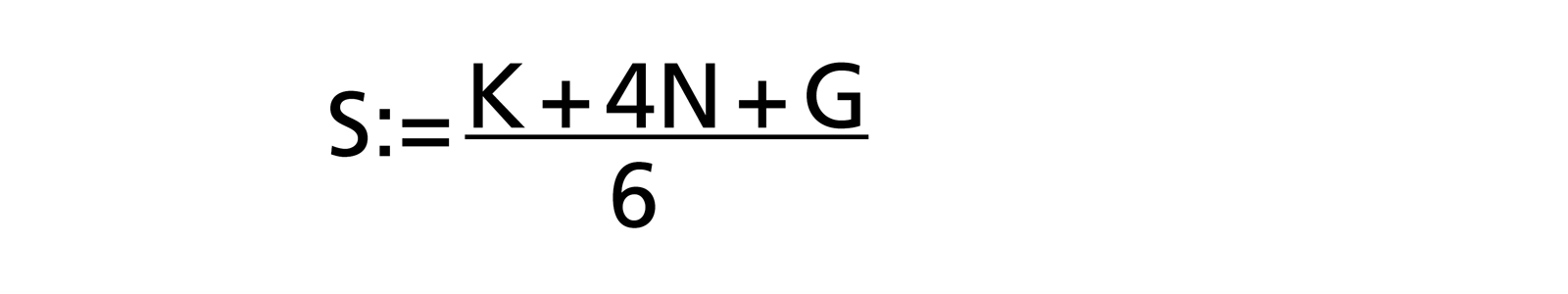
Die Erfahrung hat gezeigt, dass bei den Schätzern häufig ein Hang zum Optimismus besteht, da Aufgaben und Schwierigkeiten vergessen werden. Daher hat Barry W.  Boehm (in [R. D. Stutzke: «Estimating Software Intensive Systems», 2005, ISBN 0-201-70312-2]) dem Worst-Case-Wert G in der 3-Punkt Schätzung grösseres Gewicht gegeben, indem er ein Gewicht vom Normalfall zum Worst Case verschob:

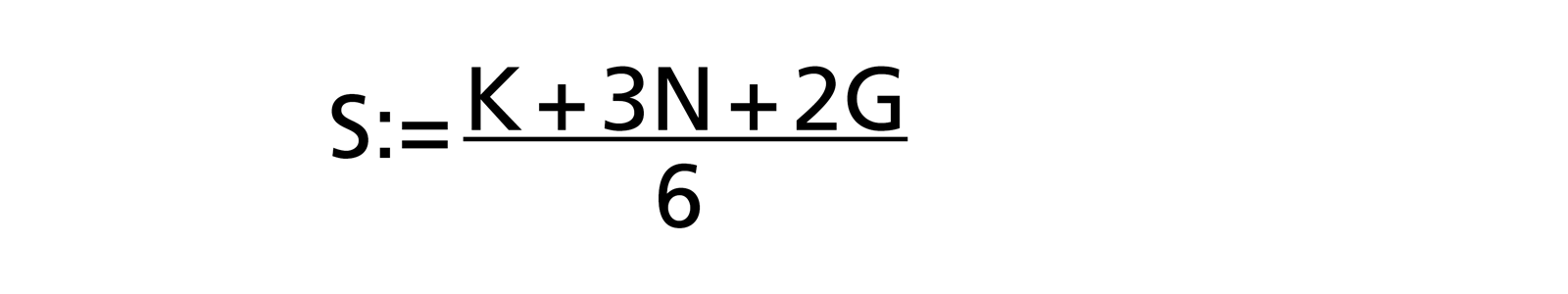
Zweipunktschätzung

Indirekt einen anderen Ansatz wählte [W. Reiter: «Die nackte Wahrheit über Projektmanagement», 2003 ISBN 3-280-05018-9], indem er in seiner Formel das Gewicht vom Optimalfall K zum Worst-Case G verschob:

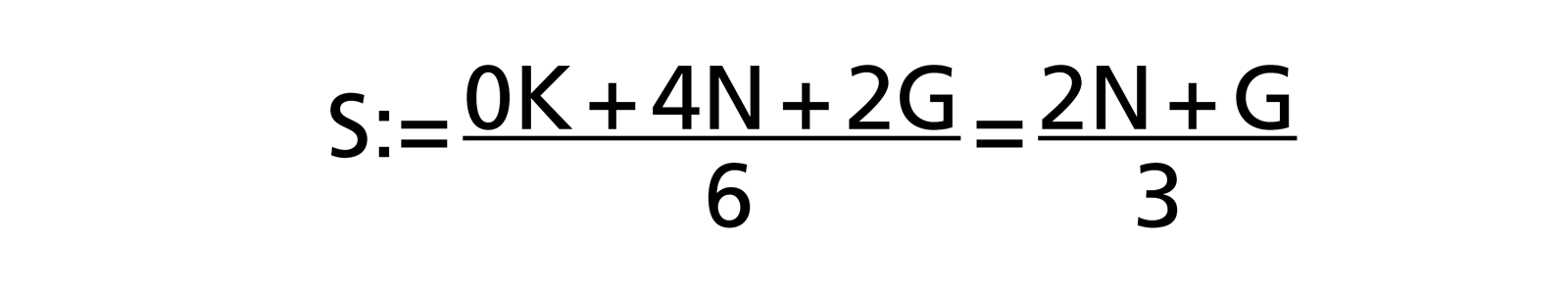
Diese Zweipunktschätzung des Aufwandes hat neben der Optimismuskorrektur den Vorteil, dass man sich einen von drei Schätzwerten und so einen Teil des Schätzaufwands sparen kann.

Optimismus? Wirklich?

In [N. N. Taleb: «Antifragile», 2012 ISBN 1-400-06782-0], im Kapitel «Why planes don't arrive early» gibt es noch eine andere, philosophische Erklärung dafür, dass Projekte immer eher unterschätzt werden. Man plant selten zu viel, je komplexer das Projekt, die Tätigkeit, desto mehr geht vergessen. Da der Zeitaufwand für solche vergessenen Tätigkeiten immer positiv ist, kann der Gesamtaufwand nur grösser werden, nie kleiner.

Begründung der Zweipunktschätzung des Aufwandes mit der Normalverteilung

Wenn einem die ganze PERT-Geschichte zu empirisch ist, kann man die obige Formel der Zweipunktschätzung des Aufwandes auch mit der Normalverteilung begründen, wie in [W. Reiter: «Die nackte Wahrheit über Projektmanagement», 2003 ISBN 3-280-05018-9], gemäss folgender Darstellung:

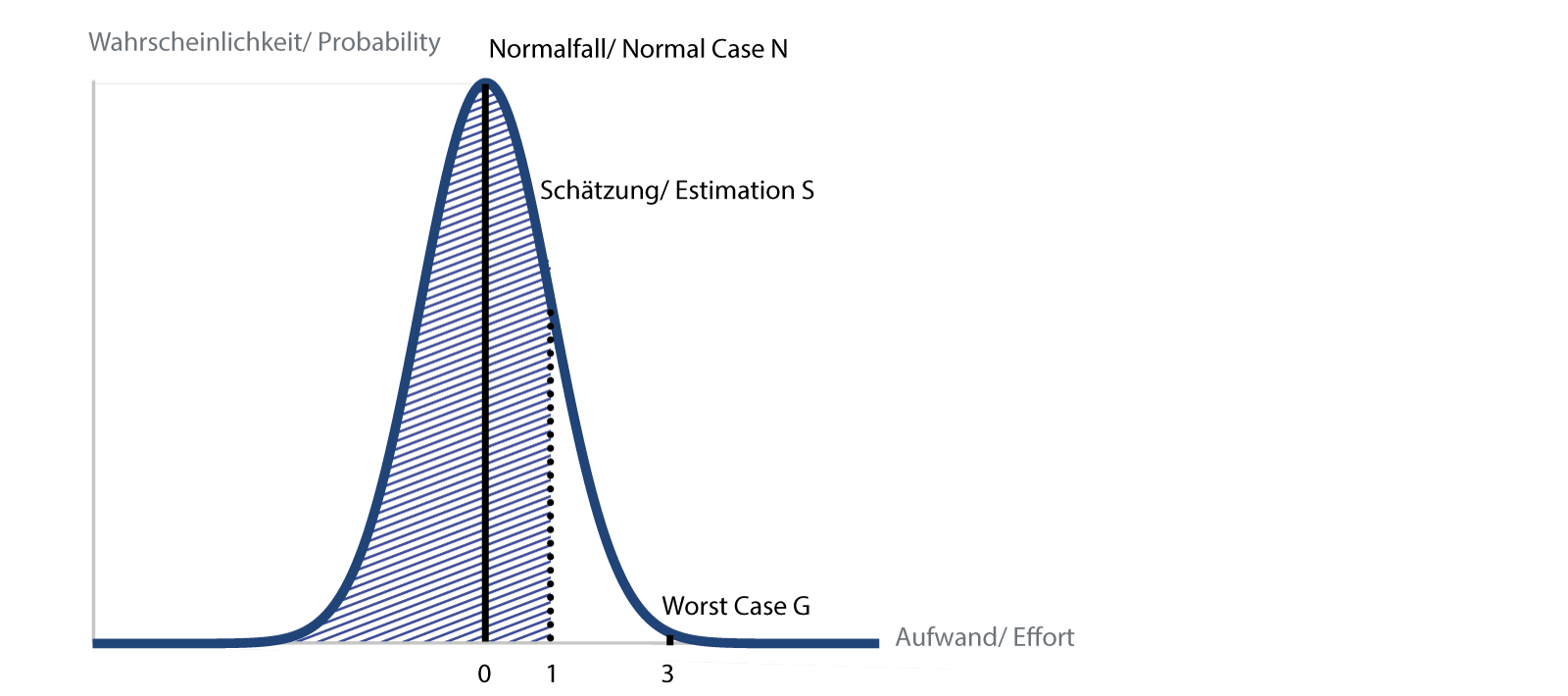
Normalverteilung mit eingetragenen Schätzwerten und der 84% Fläche

Eingetragen sind der Normalfall N und der schlechtmöglichste Fall G. Nun legen wir fest, dass wir für 99.9 % der Fälle unterhalb des Worst Case G liegen möchten. Dadurch können wir eine Normalverteilung («Gauss-Kurve») einpassen, indem der Normalfall dem Scheitelwert, das heisst dem häufigsten Fall entspricht, der Worst Case einer Abweichung von drei Standardabweichungen («3 Sigma»), der kleine Rest oberhalb entspricht dann einer Wahrscheinlich- keit von 0.1 %.

Weiter legen wir fest, dass wir in 84 % der Fälle mit unserer Schätzung unter dem Schätzwert liegen möchten. Dies entspricht einer Standardabweichung («1 Sigma»), die sich auf dem Drittel des Wegs zwischen normalem und schlechtmöglichstem Fall befindet. Als Formel ausgeschrieben:

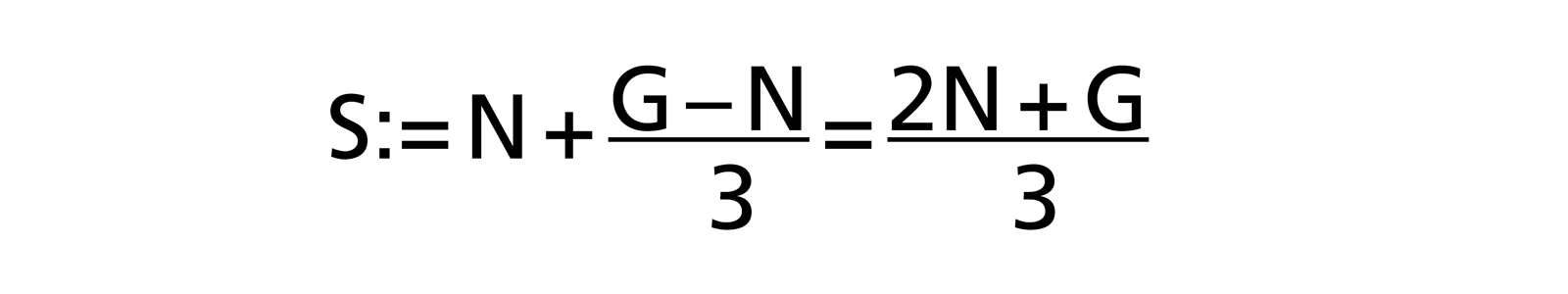
Also das gleiche Resultat wie oben. An dieser Art der Begründung unschön ist die Tatsache, dass die Normalverteilung auch negative Aufwände zulässt. Das wäre zwar für die Projektmanager manchmal schön, aber ich habe noch von niemandem gehört, der eine Arbeit fertiggestellt hat, bevor er begonnen hat.

Lognormalverteilung mit Schätzwerten

Als Modell für unsere Zwecke ist die Lognormalverteilung geeignet, da sie einerseits einen Wertbereich über null abdeckt und andererseits durch zwei Parameter vollständig charakterisiert werden kann, in unserem Fall durch den Normalwert und den Worst Case. Der Normalfall ist definiert als der Fall, wo die Wahrscheinlichkeit am grössten ist, das heisst der Scheitelwert. Der Worst-Case-Wert kann wieder bei 99.9 % gewählt werden. Wir selbst verwenden 95 %, dies ergibt auch hier eine gewisse Korrektur des Optimismus der Schätzer.

Der Erwartungswert, das heisst der Wert, den man am wahrscheinlichsten erwarten würde, ist der Mittelwert, der bei dieser Verteilung im Gegensatz zur Normalverteilung nicht mit dem Scheitelwert übereinstimmt. Der grosse Nachteil der Lognormalverteilung ist der, dass man für die Berechnung von Summen und Produkten numerische Methoden oder Monte-Carlo-Simulationen verwenden muss. Eine einfache Implementation als Tabellenkalkulation ist nicht möglich.

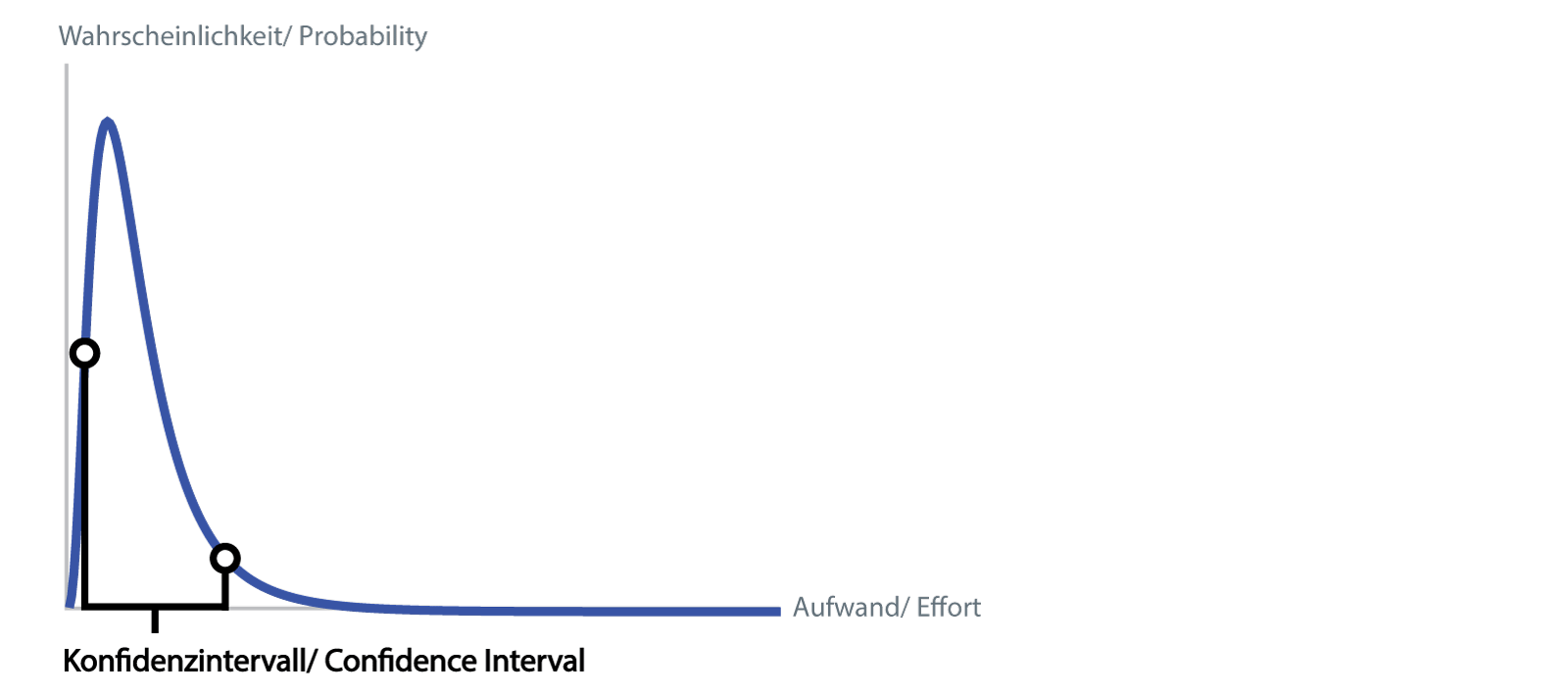
Konfidenzintervall

Anders ausgedrückt ist die Wahrscheinlichkeit 5 %, dass der Aufwand unterhalb der unteren Schwelle liegt, 5 %, dass er oberhalb der oberen Schwelle liegt. Die Breite des Konfidenzintervalls gibt zusätzlich ein gutes Mass für das Risiko des Projekts: Ein Intervall von 2000 bis 6000 Stunden deutet auf ein risikoreicheres Projekt hin als eines von 3000 bis 5000 Stunden.

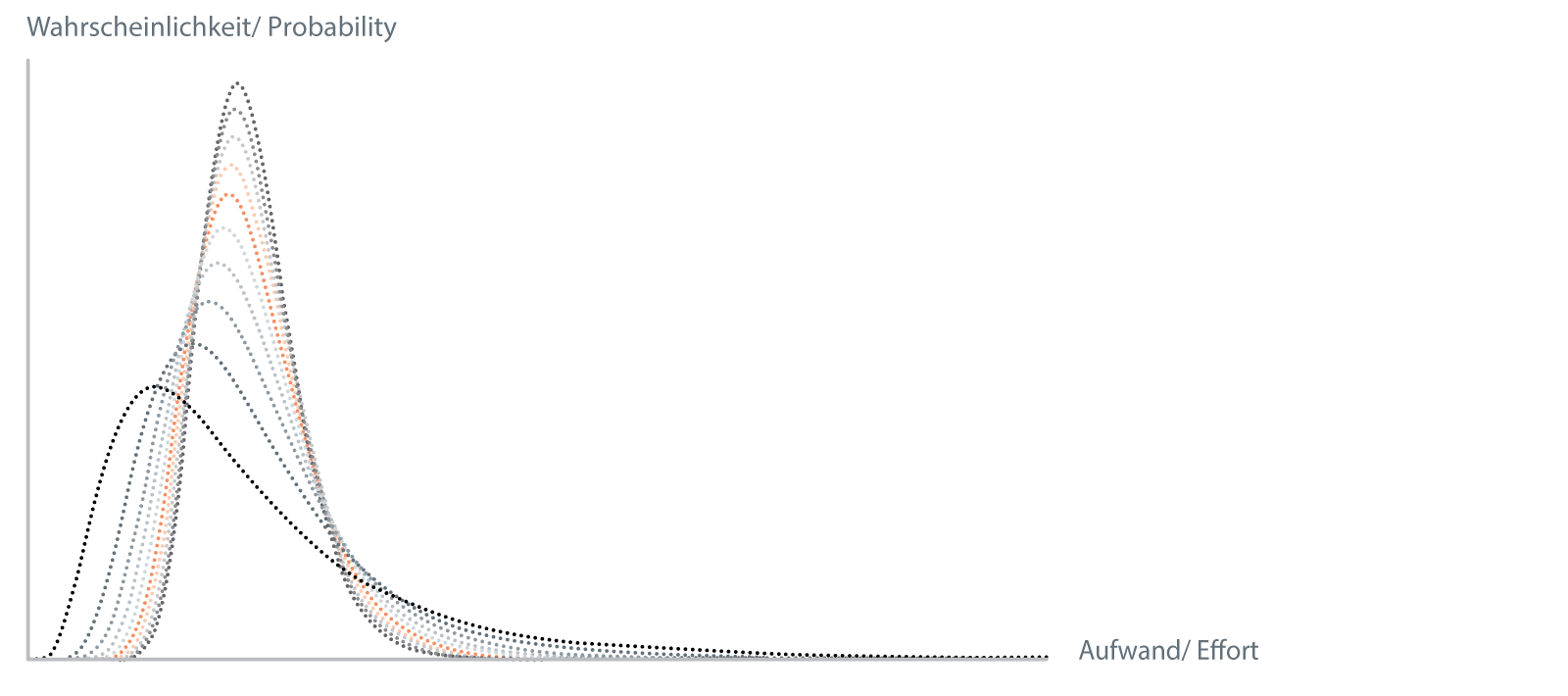
Summation von lognormal verteilten Zufallsvariablen

In obigem Bild sieht man, wie eine Lognormalverteilung zehnmal mit sich selbst gefaltet wird, was der Addition der darunterliegenden Zufallsvariablen entspricht. Die resultierende Verteilung wurde jeweils mit der Anzahl der Faltungen skaliert, so dass man sieht, wie sich die Form der Verteilung ändert.

Sofort fällt auf, wie die resultierende Verteilung bei jedem Schritt schmaler wird. Dies ist der zentrale Grenzwertsatz der Wahrscheinlichkeitsrechnung, der unter anderem besagt, dass unter verschiedenen Voraussetzungen die Verteilungsfunktion von aufsummierten Zufallsvariablen immer schmaler wird.

Die Wichtigste dieser Voraussetzungen ist für uns die Unabhängigkeit, das heisst dass sich die verschiedenen Schätzelemente nicht gegenseitig beeinflussen dürfen. Für das Projektmanagement ist das sicher falsch, da jedes geschätzte Paket, wenn es zum Beispiel länger dauert, die Gesamtdauer des Projekts verlängert und so den Aufwand für das Management des Projekts erhöht. Dieses generelle Problem lässt sich dadurch angehen, dass man solche abhängigen Pakete (z.B. Systemtests und Fehlerbehebung) erst am Schluss abschätzt, wenn der Aufwand für das ganze restliche Projekt schon bekannt ist.